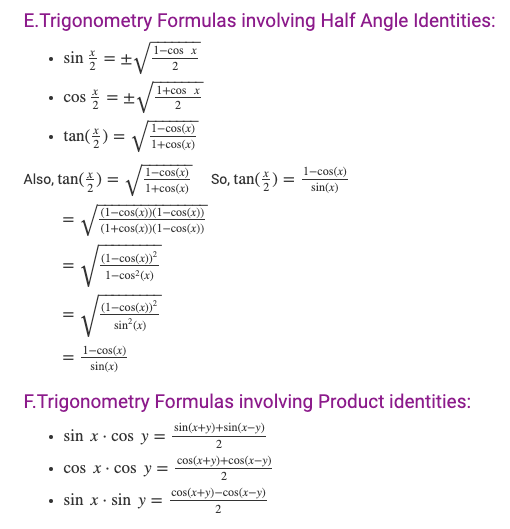
√ 1-cos x formula in terms of sin 743193-1-cos x formula in terms of sin

Cos1 (–x) = π – cos1 x;Sin(2x) = 2 sin x cos x (in terms of sin and cos) sin(2x) = (2tan x) /(1 tan 2 x) (in terms of tan) These are the main formulas of sin 2x But we can write this formula in terms of sin x (or) cos x alone using the trigonometric identity sin 2 x cos 2 x = 1 They are sin 2x = 2 √(1 cos 2 x) cos x (sin 2x formula in terms of cos) sin 2x = 2 sin x √(1 sin 2 x) (sin 2x formula in terms of sin)Sin(x y) = sinxcosy cosxsiny sin(x y) = sinxcosy cosxsiny cos(x y) = cosxcosy sinxsiny cos(x y) = cosxcosy sinxsiny tan(x y) = tanxtany 1 tanxtany tan(x y) = tanx tany 1tanxtany HalfAngle Formulas sin 2 = q 1 cos 2 cos 2 = q 1cos 2 tan 2 = q 1cos tan 2 = 1 cosx sinx tan 2 = sin 1cos DoubleAngle Formulas sin2 = 2sin cos cos2 = cos2 sin2 tan2 = 2tan 1 tan2

Summary Of Trigonometric Identities

1-cos x formula in terms of sin

1-cos x formula in terms of sin-Sec1 (–x) = π – sec1 x;What is Sin 3x Formula?

Trigonometric Functions With Their Formulas

Write sin(3x) in terms of sin(x), angle sum formula for sine, double angle formula for sine, double angle formula for cosine, simplifying trig identities, tr 1 − cosx sinx = 2sin2(x 2) 2sin(x 2)cos(x 2) = tan( x 2)Cosec1 (–x) = – cosec1 x;

Sin1 (–x) = – sin1 x;Simplify\\sin^2 (x)\cos^2 (x)\sin^2 (x) simplify\\tan^4 (x)2\tan^2 (x)1 simplify\\tan^2 (x)\cos^2 (x)\cot^2 (x)\sin^2 (x) trigonometricsimplificationcalculator en1cosx can be solved with different methods one can be used as 1cos^2(x)=sin^2(x) (1cosx)(1cos(x))=sin^2(x) so 1cosx=sin^2(x)/(1cosx) where cosx is not equals to 1

Excsc(θ) = exsec(π / 2 − θ) = csc(θ) − 1; sin1 (x) = sin1 (x), x ∈ 1, 1 2 cos1 (x) = π cos1 (x), x ∈ 1, 1 3 tan1 (x) = tan1 (x), x ∈ R 4 cosec1 (x) = cosec1 (x), x ≥ 1 5 sec1 (x) = π sec1 (x), x ≥ 1 6 cot1 (x) = π – cot1 (x), x ∈ R 7 sin1 x cos1 x = π/2 , x ∈ 1, 1 8 tan1 x cot1 x = π/2 , x ∈ R 9 sec1 x cosec1 x = π/2 ,x ≥ 1 10The functions sin x and cos x can be expressed by series that converge for all values of x These series can be used to obtain approximate expressions for sin x and cos x for small values of x The trigonometric system 1, cos x, sin x, cos 2x, sin 2x, , cos nx, sin nx, constitutes an orthogonal system of functions on the interval

Can Someone Explain To Me How Sin X Cos H Cos X Sin H Sin X Sin X Cos H Sin X Cos X Sin H R Askmath

How To Solve The Equation 1 Cosx Tanx Sinx Quora

Sin(sin 1(x)) 2 cos(sin 1(x)) 2 = 1 x2 cos(sin 1(x)) 2 = 1 cos(sin 1(x)) 2 = 1 x2 cos(sin 1(x)) = p 1 x2 Now the question is Which do we choose, p 1 x2, or p 1 x2, and this requires some thinking!And the cosecant of x is defined to be 1 divided by the sine of x cscx = 1 sinxThe Pythagorean identity of sine and cosine functions is also written popularly in two other forms $\sin^2{x}\cos^2{x} \,=\, 1$ $\sin^2{A}\cos^2{A} \,=\, 1$ Remember, the angle of right triangle can be denoted by any symbol but the relation between sine and cosine functions should be expressed in that symbol Proof Learn how to derive the

Integrate Sin 22x Cos 22x

Addition Identities

Y = sin x d y d x = cos x d 2 y d x 2 = − sin x d 3 y d x 3 = − cos x d 4 y d x 4 = sin x y = sin x d y d x = cos x d 2 y d x 2 = − sin x d 3 y d x 3 = − cos x d 4 y d x 4 = sin x Analysis Once we recognize the pattern of derivatives, we can find any higherorder derivative by determining the step in the pattern to which it correspondsOne third angle formulas Learn how to expand trigonometric functions in terms of one third angle trigonometric functions ( 1) sin ⁡ θ = 3 sin ⁡ ( θ 3) − 4 sin 3 ⁡ ( θ 3)$\cos x = 1 2 * \sin^2(x/2)$ prove \begin{align} &=>1 2 * \sin^2(x/2) \\ &= 1 2 * \sin(x/2) * \sin(x/2) \\ &= 1 2 * \sqrt{((1\cos x)/2)} * \sqrt{((1\cos x)/2)} \quad \text{NOT even sqrts are (), ()*()=()} \\ &= 1 2 * (1\cos x)/2 \\ &= 1 1 \cos x \\ &= \cos x \\ \end{align}

Cosine Formula What Are Cosine Formulas Examples

2

Cos 2x = 2 cos 2 x 1;By using identity $\sin^2 x = 1 \cos^2 x$, we can change $\sin^4 x$ to $$\sin^4 x = (1\cos^2 x)^2$$ $\cos^2 x$ can be changed by using identity $\cos 2x= 2\cos^2 x1$, then $\cos^2 x = \frac {1\cos 2x} {2}$ So, $\sin^4 x = (1\frac12\frac12\cos 2x)^2$Versin(θ) = 1 − cos(θ) = 2 sin 2 (θ / 2) coversin(θ) = 1 − sin(θ) = versin(π / 2 − θ) haversin(θ) = 1 / 2 versin(θ) = sin 2 (θ / 2) exsec(θ) = sec(θ) − 1;

Answered 26 Y 5 Cos X 3d 25 Y 10 Sin X Bartleby

Solved 12 Consider The Following Formula Sin Nx Chegg Com

 Let's see how we can learn it 1In sin, we have sin cos In cos, we have cos cos, sin sin In tan, we have sum above, and product below 2For sin (x y), we have sign on right For sin (x – y), we have – sign on right right For cos, it becomes opposite For cos (x y), weSin 3x is the sine of three times of an angle in a rightangled triangle, that is expressed as Sin 3x = 3sin x – 4sin 3 xSolve it for cos y in terms of sin y, and then replace sin y by x Don't be too hasty with that formula for cos y Solving for cos y involves a square root, and we need to know whether to take the positive or negative square root The following figures show the graph of cos y (with y as independent variable) in red and the graph of the positive

3

Power Reducing Formulas And How To Use Them With Examples Owlcation

0 Some common Identities and formulas generally used in finding Trigonometric ratios are stated below Double or Triple angle identities 1) sin 2x = 2sin x cos x 2) cos2x = cos²x – sin²x = 1 – 2sin²x = 2cos²x – 1 3) tan 2x = 2 tan x / (1tan ²x) 4) sin 3x =Along the unit circle by an angle , taking (in terms of real coordinates) (1;0) !(cos ;sin ) This is also true for the point z= i, which gets taken to i(cos isin ) = sin icos In terms of real coordinates on the plane, this is (0;1) !( sin ;cos ) and the rotation looks like this 5 `sin^2(α/2) = (1 − cos α)/2` Solving gives us the following sine of a halfangle identity `sin (alpha/2)=sqrt((1cos alpha)/2` The sign (positive or negative) of `sin(alpha/2)` depends on the quadrant in which `α/2` lies If `α/2` is in the first or second quadrants, the formula uses the positive case `sin (alpha/2)=sqrt(1cos alpha)/2`

Math34 Trigonometric Formulas

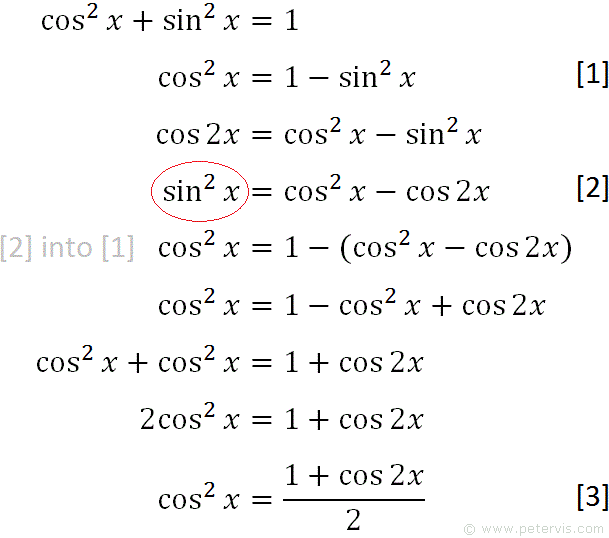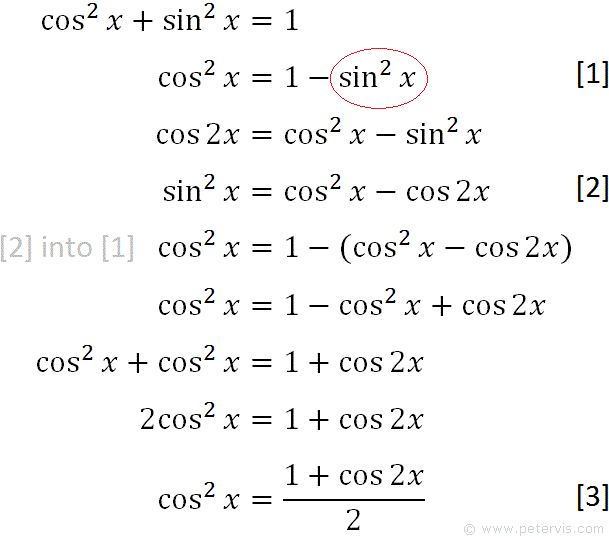
Integrate Sin 22x Cos 22x

The functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions Their usual abbreviations are ⁡ (), ⁡ (), and ⁡ (), respectively, where denotes the angle The parentheses around the argument of the functions are often omitted, eg, ⁡ and ⁡, if an interpretation is unambiguously possible The sine of an angle is defined1(t) = A 1 cos(w 0t˚ 1), x 2(t) = A 2 cos(w 0t˚ 2), and x(t) = x 1(t)x 2(t) Then x(t) = Acos(w 0t˚) and the phasor representation for x(t) is X= Aej˚= A 1e j˚ 1 A 2e j˚ 2 ContinuousTime Unit Impulse and Unit Step Z 1 1 (t)dt= 1 Z 1 1 x(t) (t)dt= x(0) Z 1 1 x(t) (t t 0)dt= x(t 0) u(t) = Z t 1 (t)dt 2Sin hypotenuse q= hypotenuse csc opposite q= adjacent cos hypotenuse q= hypotenuse sec adjacent q= opposite tan adjacent q= adjacent cot opposite q= Unit circle definition For this definition q is any angle sin 1 y q==y 1 csc y q= cos 1 x q==x 1 sec x q= tan y x q= cot x y q= Facts and Properties Domain The domain is all the values of q that can be plugged into the function

Solved 7 Tt Rewrite Cos X 4 In Terms Of Sin X And Cos A Cos 2 Sina X Submit Question Question 14 2 5 5 Pts 2 0 Details Score On Last Course Hero

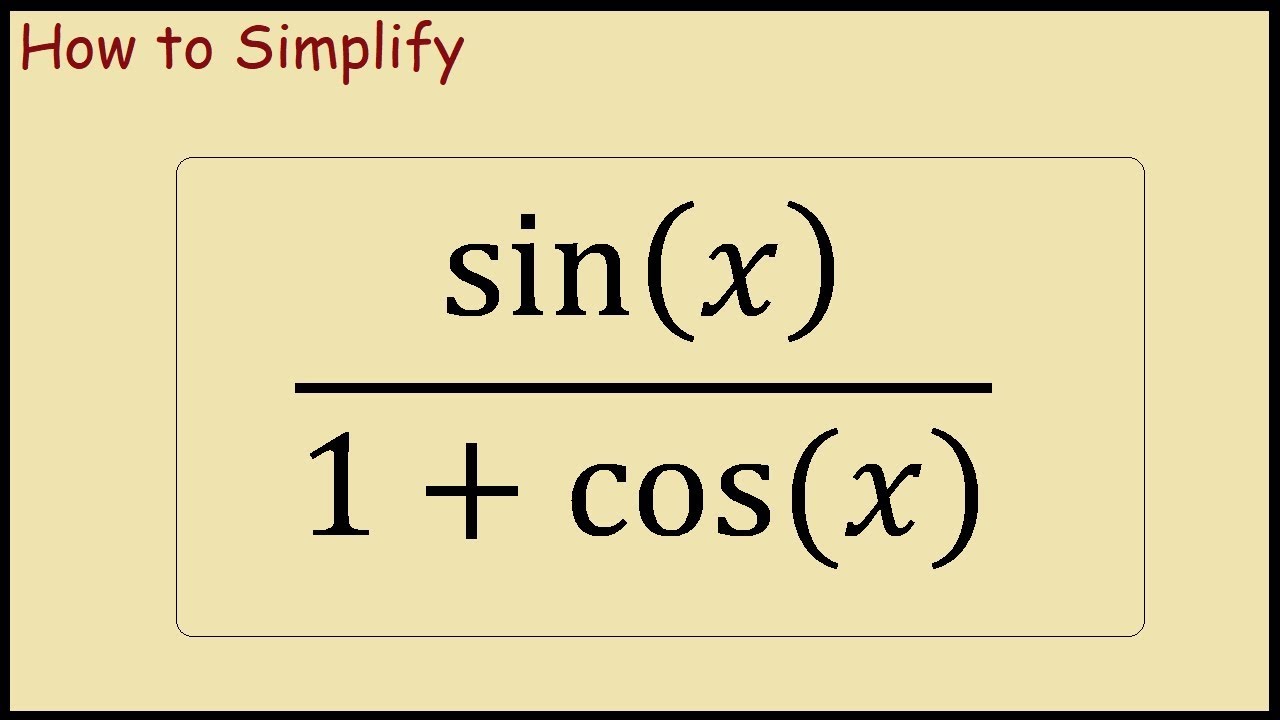
How To Simplify Sinx 1 Cosx Youtube

Sin x = √(1 cos 2 x) Using the above formulas, we have tan 2x = sin 2x/ cos 2x = 2 sin x cos x/(2 cos 2 x 1) = 2 cos x/(2 cos 2 x 1)√(1 cos 2 x)We can derive the tan 2x formula in terms of cos We will use the following trigonometric formulas to express tan 2x in terms of cos x tan x = sin x/ cos x;Sin ^2 (x) cos ^2 (x) = 1 tan ^2 (x) 1 = sec ^2 (x) cot ^2 (x) 1 = csc ^2 (x) sin(x y) = sin x cos y cos x sin y cos(x y) = cos x cosy sin x sin y

Anti Derivative Of Csc Pdf Integral Trigonometric Functions

Ex 13 1 17 Evaluate Lim X 0 Cos2x 1 Cosx 1 Ex 13 1 Term

Tan1 (–x) = – tan1 x;The thing is We defined sin 1(x) to have range ˇ 2;Cosine 2X or Cos 2X is also, one such trigonometrical formula, also known as double angle formula, as it has a double angle in it Because of this, it is being driven by the expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions Let us start with the cos two thetas or cos 2X or cosine

Trigonometric Functions With Their Formulas

21 Differentiation And Integration Of Trigonometry Function 9709

EULER'S FORMULA FOR COMPLEX EXPONENTIALS According to Euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definitioneit = cos ti sin t where as usual in complex numbers i2 = ¡1 (1) The justification of this notation is based on the formal derivative of both sides, The value of the tan function for any angle θ in terms of sin and cos can be given using the formula, tan θ = sin θ/cos θ Also, What is the formula of trigonometry?Cot1 (–x) = π – cot1 x;

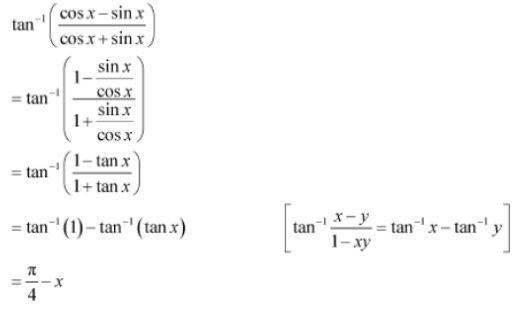
Write The Function In The Simplest Form Tan 1 Cos X Sin X Cos X Sin X 0 X P Cbse Class 12 Maths Learn Cbse Forum

All Elementary Mathematics Study Guide Trigonometry Trigonometric Equations Main Methods For Solving

The Pythagorean formula for sines and cosines sin 2 t cos 2 t = 1 Identities expressing trig functions in terms of their complements cos t = sin(/2 – t) sin t = cos(/2 – t) cot t = tan(/2 – t) tan t = cot(/2 – t) csc t = sec(/2 – t) sec t = csc(/2 – t) Periodicity of trig functionsSin(x)cos(x)=1 Square both sides of the equation Rewrite as Expand using the FOIL Method Move all terms not containing to the right side of the equation Replace with in the formula for period Solve the equation 6 Expressing a sin θ ± b cos θ in the form R sin(θ ± α) by M Bourne In electronics, we often get expressions involving the sum of sine and cosine terms It is more convenient to write such expressions using one single term

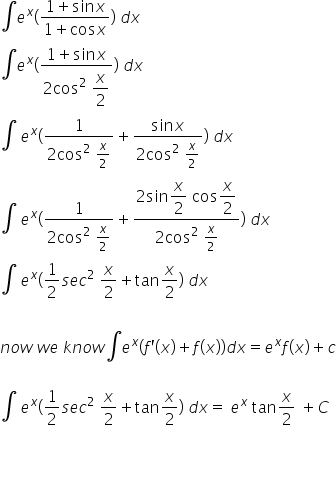
Integration Ex 1 Sin X 1 Cos X Dx Explain In Great Detail Mathematics Topperlearning Com Ejafs0yy

Tangent Half Angle Formula Wikipedia

If you have gone through doubleangle formula or tripleangle formula, you must have learned how to express trigonometric functions ofSin 2x = 2 sin x cos x;Expressing sin (x±y) and cos (x±y) in terms of sinx, siny, cosx & cosy and their simple application Cos (x y) × cos y sin (x y) × sin y = cos x Firstly, we will be using the trigonometric identities As we know that Cos (ab) = cosa × cosb – sinxa × sinb Sin (ab) = sina × cosb sina × cosb

What Are The Formulas Of Cos 2x Quora

X Y X Y X Y X Y Sect 5 1 Verifying Trig Identities Reciprocalco Function Quotient Pythagorean Even Odd Ppt Download

Relations between cosine, sine and exponential functions (45) (46) (47) From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that were immensely painful to prove back in high schoolFunctions are derived in some way from sine and cosine The tangent of x is defined to be its sine divided by its cosine tanx = sinx cosx The cotangent of x is defined to be the cosine of x divided by the sine of x cotx = cosx sinx The secant of x is 1 divided by the cosine of x secx = 1 cosx; It would be nice to have a formula for cos 2A in terms of just a sine or just a cosine Fortunately, we can use sin² x cos² x = 1 to eliminate either the sine or the cosine from that formula cos 2A = cos² A − sin² A = cos² A − (1 − cos² A) = 2 cos² A − 1

Art Of Problem Solving

Tangent Half Angle Formula Wikipedia

To see the answer, pass your mouse over the colored area To cover the answer again, click "Refresh" ("Reload")It says that c 2 , the square of one side of the triangle, is equal to a 2 b 2 , the sum of the squares of the the other two sides, minus 2ab cos C, twice their product timesCosec x = 1 sin x cot x = 1 = cos x tan x sin x Note, sec x is not the same as cos1 x (sometimes written as arccos x) Remember, you cannot divide by zero and so these definitions are only valid when the denominators are not zero Example If sec x = 2, cos x

Weierstrass Substitution Wikipedia

6 3 Reduction Formula Trigonometry Siyavula

1 tanutanv Double Angle Formulas sin(2u) = 2sinucosu cos(2u) = cos2 u sin2 u = 2cos2 u 1 = 1 22sin u tan(2u) = 2tanu 1 tan2 u PowerReducing/Half Angle Formulas sin2 u= 1 cos(2u) 2 cos2 u= 1cos(2u) 2 tan2 u= 1 cos(2u) 1cos(2u) SumtoProduct Formulas sinusinv= 2sin uv 2 cos u v 2 sinu sinv= 2cos uv 2 sin u v 2 cosucosv= 2cos uv 2 cos u Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin ⁡ \sin sin andWrite the trigonometric expression in terms of sine and cosine, and then simplify cos t csc t 2 Question Details SPreCalc6 Use an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1 Find sin 2 x, cos 2 x, and tan 2 x from the given information sin 2 x= cos 2 x= tan 2 x

Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube

Copyright C Cengage Learning All Rights Reserved Ppt Download

The first shows how we can express sin θ in terms of cos θ;Find stepbystep Calculus solutions and your answer to the following textbook question Express cos 3x in terms of sin x and cos xˇ 2 so, cos(sin 1(x)) has range 0;1, and is in particular 0 (see picture below for

What Is The Formula Of 1 Cos2x Quora

Euler S Formula Wikipedia

The second shows how we can express cos θ in terms of sin θ Note sin 2 θ "sine squared theta" means (sin θ) 2 Problem 3 A 345 triangle is rightangled a) Why?Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions Ptolemy's identities, the sum and difference formulas for sine and cosine Double angle formulas for sine and cosine Note that there are three forms for the double angle formula for cosine You only need to know one, but be able to derive the

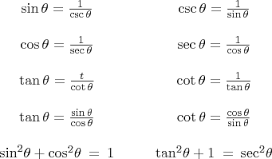
Math Review Of Trigonometric Identities Free Homework Help

Answered Sintheta 1 Cos Theta Brainly In

Summary Of Trigonometric Identities

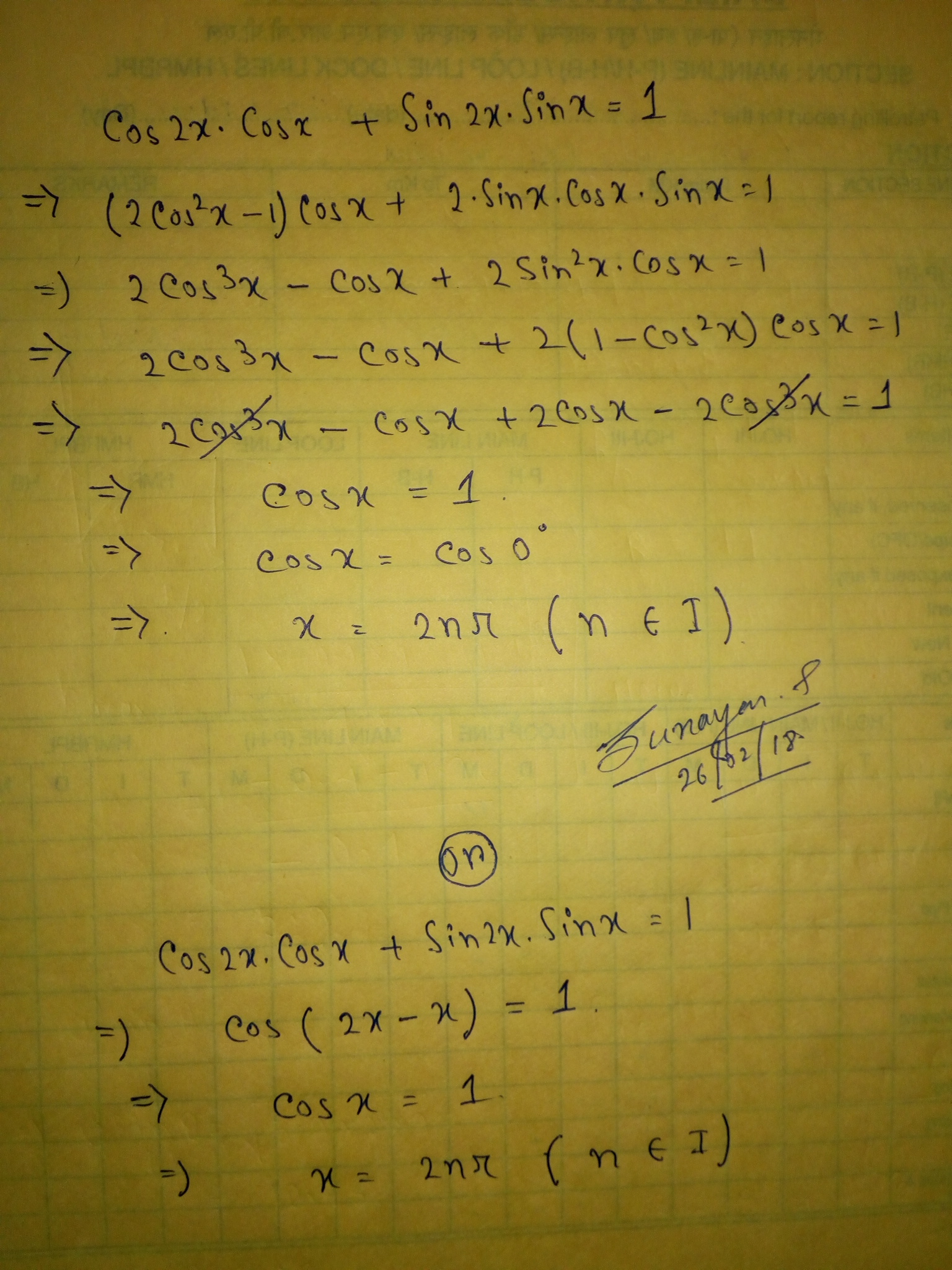
How Do You Solve Cos 2x Cos X Sin 2x Sin X 1 For All Solutions Socratic

1 Cos Theta 1 2 Solve For Interval 0 Less Theta Less 2pi Youtube

Proving Left Frac 1 Sin X I Cos X 1 Sin X I Cos X Right N Cos N Left Frac Pi 2 X Right I Sin N Left Frac Pi 2 X Right Mathematics Stack Exchange

How Do You Simplify Sinx 1 Cosx 1 Cosx Sinx Socratic

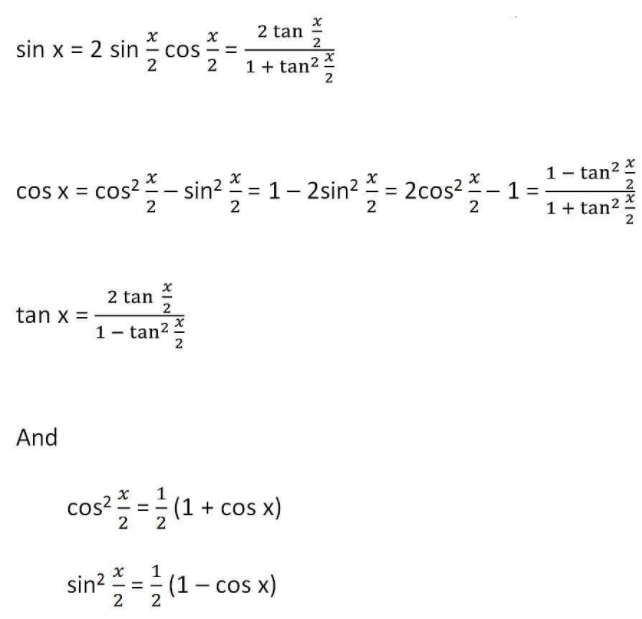
Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec

For The Differential Equations Find The General Solution Dy Dx 1 Cos X 1 Cos X Mathematics Shaalaa Com

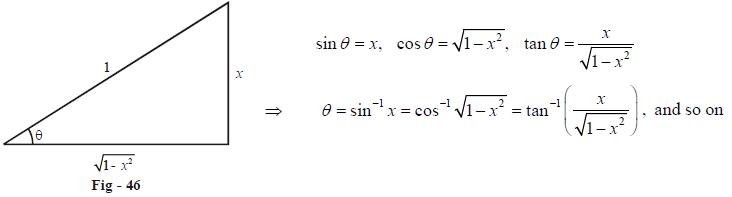
Interconversion Between Inverse Trigonometric Ratios What Is Interconversion Between Inverse Trigonometric Ratios Examples Solutions Cuemath

Solved 1 Use The Euler S Formula To Show That I Cos X Chegg Com

Solved 2 Prove The Following Identities A 1 Cosx Sinx Chegg Com

1

Trigonometric Identity Sinx 1 Cos 1 Cosx Sinx Youtube

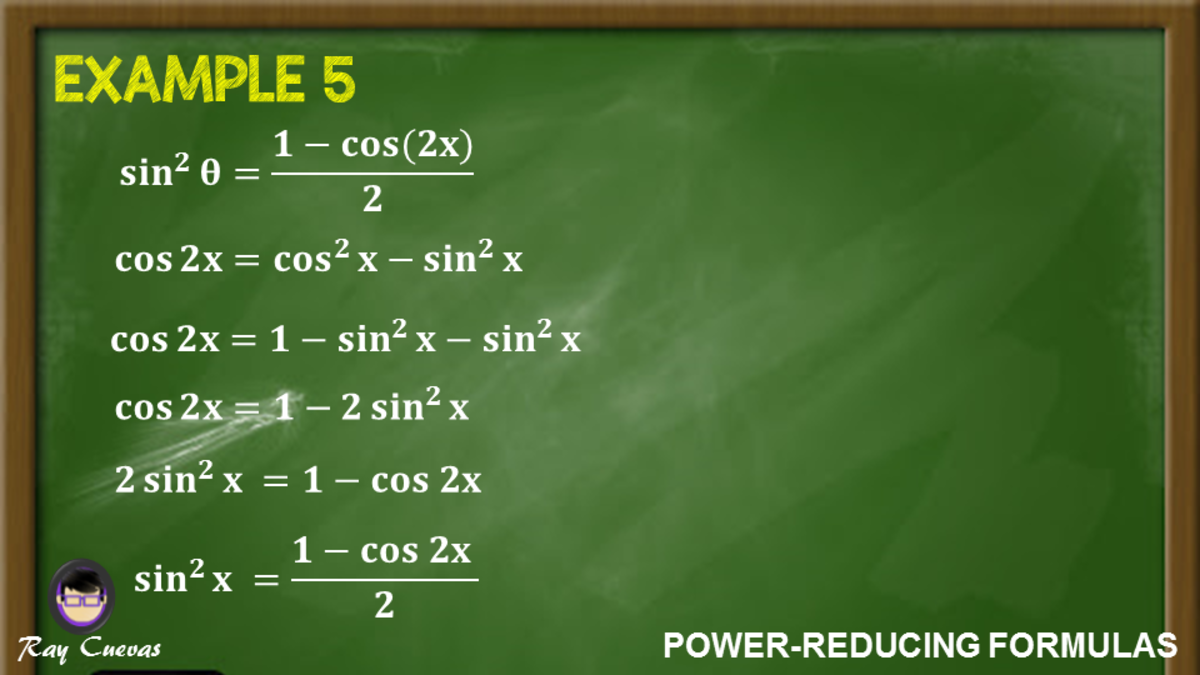
Power Reducing Formulas And How To Use Them With Examples Owlcation

Chapter 2 Maths 3

Trigonometric Identities Topics In Trigonometry

Solved Evaluate The Following Integrals A ſxe Dx B Chegg Com

What Is The Formula Of 1 Cosx Quora

Limit Of 1 Cos X X As X Approaches 0 Video Khan Academy

Ex 7 3 8 Integrate 1 Cos X 1 Cos X Chapter 7 Class 12

Double Angle Identities Trigonometry Socratic

Verify The Trig Identity 1 Cos X Sin X Csc X Cot X Youtube

Solved A Establish De Moivre S Formula Cos X Sin X Cos Nx I Sin Nx Where V 1and Is Positive Integer B Using The Formula Of A Express

38 Solved Questions Of Trigonometry For Trigonometric Identities Trigonometric Identities Trigonometry Sci Pi

Express In The Simplest Form Tan 1 Cos X Sinx Cosx Sin X

What Is The Square Root Of 1 Cosx Quora

Solve Trigonometric Equation 3 1 Cos X 3 1 Sin X 2 Youtube

Ex 7 6 18 Integrate E X 1 Sin X 1 Cos X Teachoo

Trigonometric Identities Ppt Download

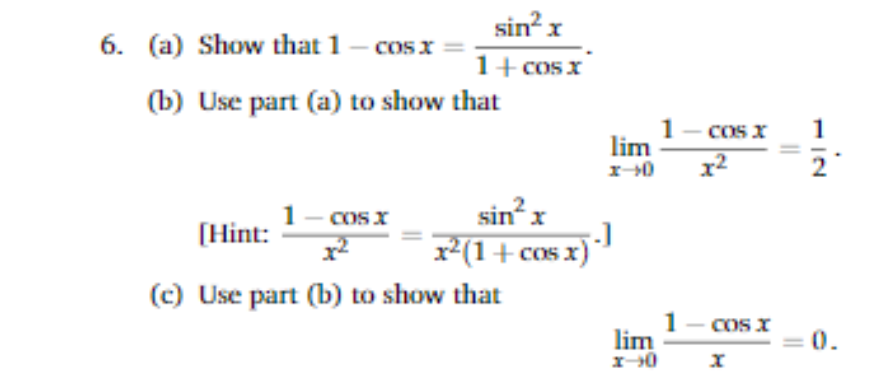
Answered Sin X 1 Cosx B Use Part A To Show Bartleby

Section 7 3 Double Angle Half Angle And Sum

Example 5 Express Tan 1 Cos X 1 Sin X Chapter 2 Inverse

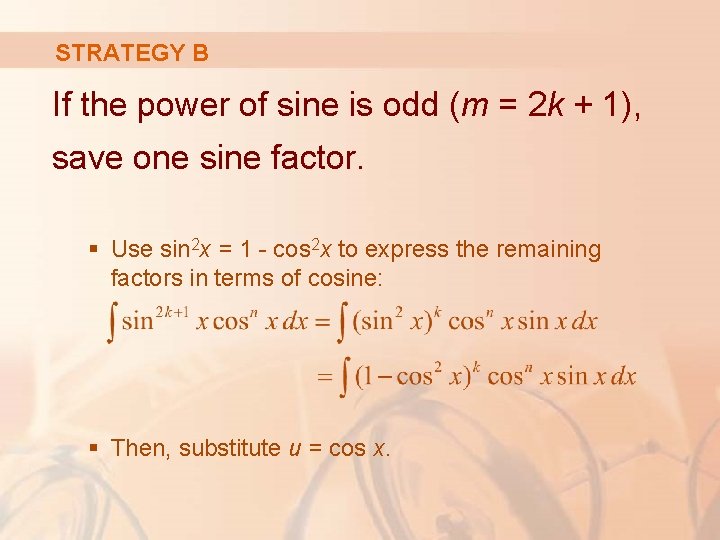
7 Techniques Of Integration Techniques Of Integration 7

What Is The Value Of 1 Cos Theta Quora

Misc 25 Evaluate Definite Integral Ex 1 Sin X 1 Cos X

3

Finding The Derivative Of 1 Cos X Video Lesson Transcript Study Com

Ex 9 4 1 Find General Solution Dy Dx 1 Cos X 1 Cosx

Write In The Simplest Form Tan 1 Cos X 1 Sin X X P 2 P 2 Sarthaks Econnect Largest Online Education Community

Trigonometric Identities A Plus Topper

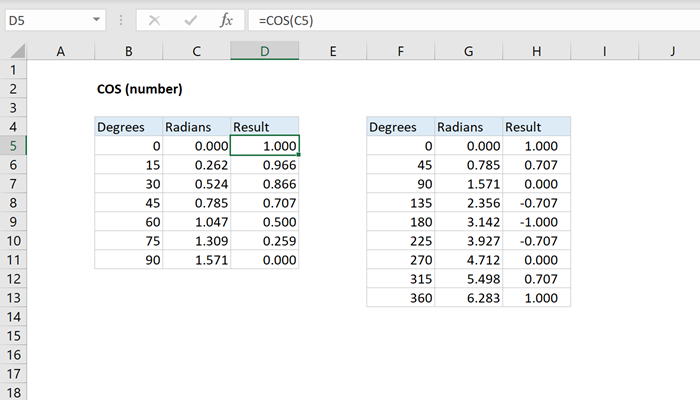
How To Use The Excel Cos Function Exceljet

1

Solved You May Use Any Appropriate Derivative Formulas For Chegg Com

Show That 1 Cos X 3 2 1 Cos X 1 2 Sin X 1 Cos X Mathematics Topperlearning Com Lr06xc66

If Sin X Cos X Sqrt Y 1 Y Such That X Belongs To 0 6 And Y 0 Prove That X 4 Or 9 4 Mathematics Topperlearning Com 05uzrgg

Basic Trigonometric Identities Ppt Download

Derivatives Of Sin X Cos X Tan X Eˣ Ln X Video Khan Academy

Ppt Reciprocal Trigonometry Functions Powerpoint Presentation Free Download Id

Ex 9 4 1 Find General Solution Dy Dx 1 Cos X 1 Cosx

Summary Of Trigonometric Identities

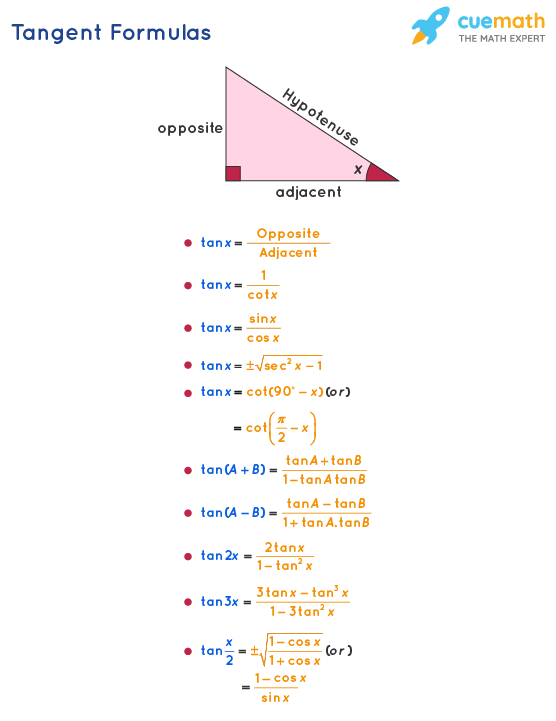
Tangent Formula What Are Tangent Formulas Examples

Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf

Lesson 24 Double Angle Half Angle Identities Ppt Video Online Download

14 2 Trigonometric Identities

Trig Integrals Trig Substitution

Ipe Material Notes

Cos 2x Formula Derivation Examples What Is Cos 2a Formula

Finding The Derivative Of 1 Cos X Video Lesson Transcript Study Com

Ex 7 3 12 Integrate Sin2 X 1 Cos X Class 12 Cbse

Finding The Derivative Of 1 Cos X Video Lesson Transcript Study Com

The Application Of The Basic Strategy For Solving Trigonometric Equations

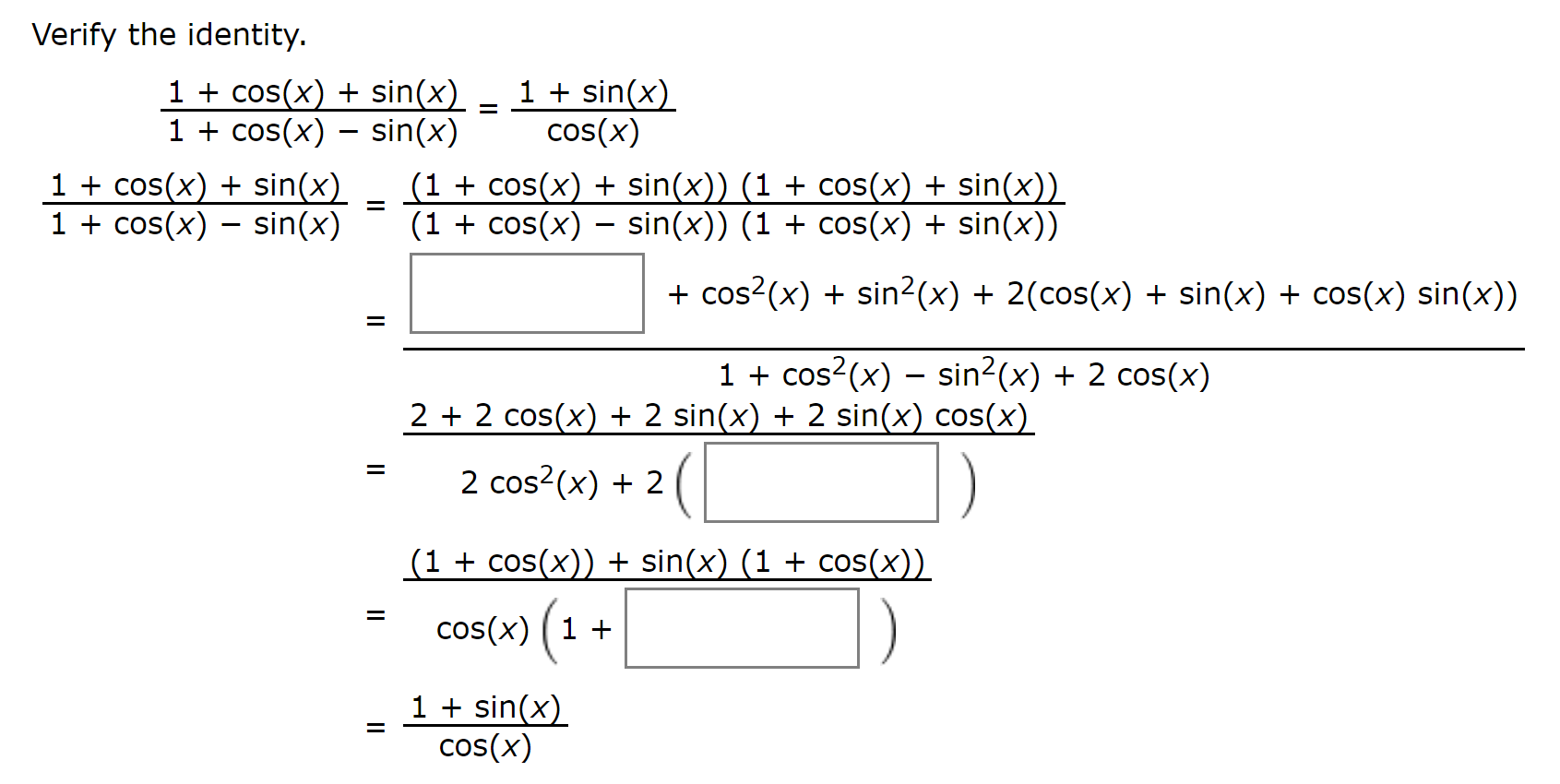
Answered Verify The Identity 1 Cos A Sin A Bartleby

Example 5 Express Tan 1 Cos X 1 Sin X Chapter 2 Inverse

Summary Of Trigonometric Identities

Example 5 Verify A Trigonometric Identity Verify The

Lesson 5 3 Solving Trigonometric Equations Solving Trigonometric

Power Reducing Formulas And How To Use Them With Examples Owlcation

Prove The Identity Cos X 1 Sin X Tan P 4 X 2 Sarthaks Econnect Largest Online Education Community

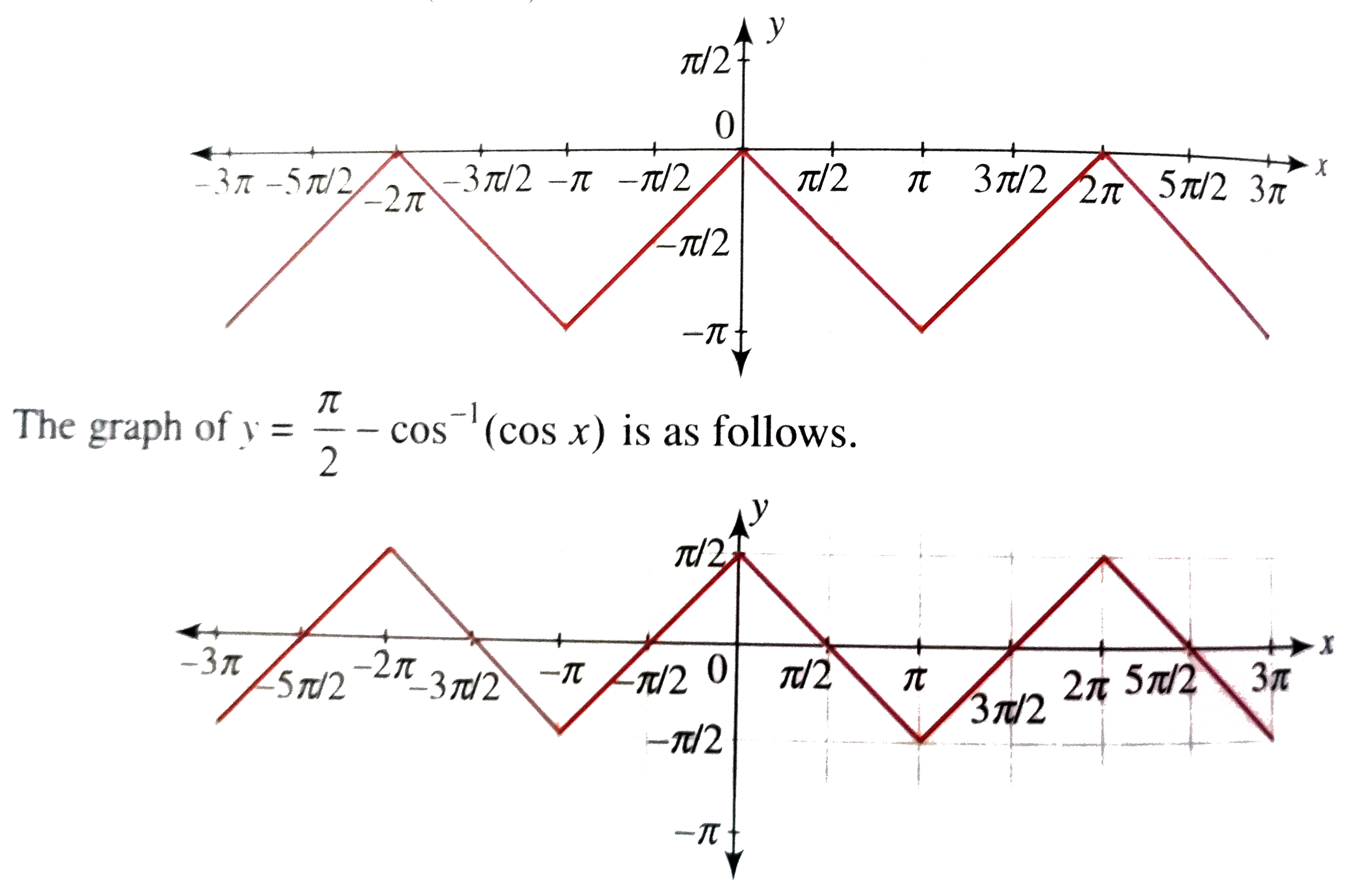
Draw The Graph Of Y Sin 1 Cosx

2 Sin Inverse X Formula In Terms Of Tan Isiah Norbert

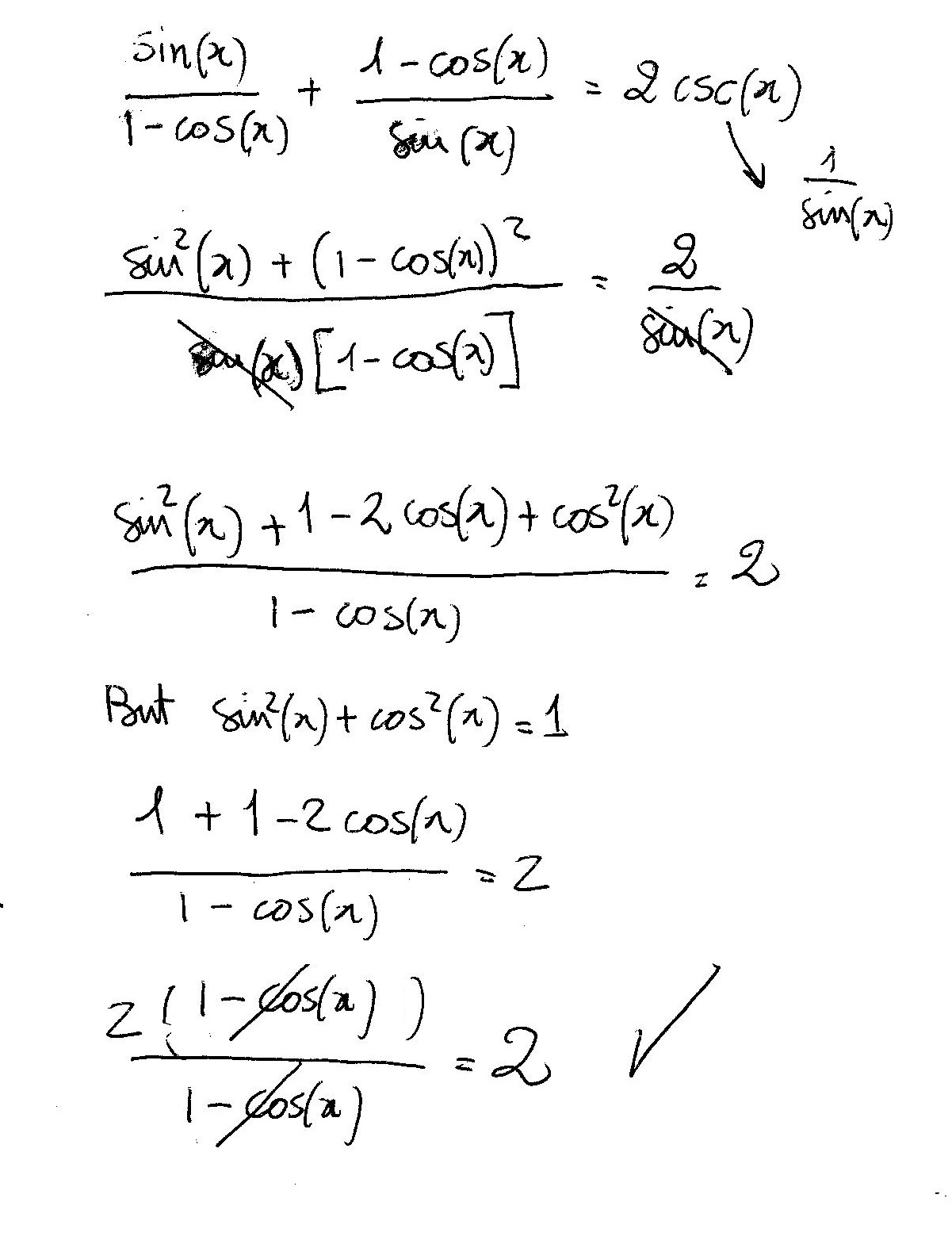
How Do You Verify Sin X 1 Cos X 1 Cos X Sin X 2csc X Socratic

Incoming Term: 1-cos x formula in terms of sin,